| Classwise Concept with Examples | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Construction of Circle & Line Segment | Construction of Perpendicular | Construction of Angles |
Chapter 14 Practical Geometry (Concepts)
Welcome to Chapter 14: Practical Geometry! While previous chapters focused on understanding the properties and names of shapes, this chapter is all about doing geometry – it's hands-on! We will learn how to draw shapes and lines accurately using specific geometric tools. Think of it like being a geometric architect or designer. The main tools we'll use are the ruler (or straightedge, primarily for drawing straight lines) and the compasses (for drawing circles and arcs, and transferring lengths). The goal isn't just to draw, but to construct geometric figures precisely based on given information and understand the steps involved. These skills are fundamental in design, engineering, art, and many other practical areas.
We will learn several fundamental constructions, following clear, step-by-step instructions. Don't worry, each step will be explained carefully, often with diagrams to help you visualize:
- Constructing a Circle: If you know the radius (the distance from the center to the edge), how do you draw a perfect circle? We'll learn how to use the compasses: set its width equal to the given radius using a ruler, fix the pointy end at the center point, and swing the pencil end around to draw the circle.
- Constructing a Line Segment of a Given Length: This involves using your ruler carefully to draw a line segment that is exactly the required length (e.g., 5.3 cm).
- Constructing a Copy of a Given Line Segment: Sometimes, we need to create a new line segment that is exactly the same length as another one, without even measuring the first one with a ruler! We'll learn how to use compasses to "pick up" the length of the original segment and transfer it accurately onto a line or ray by marking an arc.
- Constructing the Perpendicular Bisector of a Line Segment: This is a very important construction! It means drawing a line that cuts another line segment exactly in half (bisects it) and is also at a perfect right angle (perpendicular) to it. We'll learn the classic compass-and-ruler method: draw arcs with the same radius (make sure the radius is more than half the segment length!) from each endpoint, both above and below the segment. Then, connect the points where the arcs intersect. This line is the perpendicular bisector.
- Constructing the Bisector of an Angle: Just like we can bisect a line segment, we can also bisect an angle (cut it exactly in half). We'll learn the compass method: draw an arc from the vertex that cuts both arms of the angle. Then, from these two points on the arms, draw two more intersecting arcs inside the angle. The line joining the vertex to this intersection point is the angle bisector.
- Constructing Angles of Specific Measures (without a protractor!): This is where geometry gets really clever! We can construct certain angles very accurately using just a ruler and compasses. We will learn how to construct:
- A 60° angle (related to equilateral triangles).
- A 90° angle (a right angle, often by constructing a perpendicular).
- Then, by bisecting these angles, we can construct others like 30° (bisecting 60°), 120° (60°+60°), and 45° (bisecting 90°).
Throughout this chapter, remember that accuracy and neatness are important in practical geometry. Use a sharp pencil, handle your ruler and compasses carefully, and follow the sequence of steps precisely. By practicing these fundamental constructions, you'll develop valuable skills in geometric drawing and gain a deeper appreciation for the precision and logic inherent in geometry.
Construction of Circle & Line Segment
Practical Geometry is the branch of geometry that deals with the actual drawing of geometric shapes and figures using standard geometric tools. While we can draw shapes freehand, using tools helps us create accurate figures with specific measurements and properties. This chapter introduces you to using common geometry tools for basic constructions.
Tools Used in Practical Geometry
To perform constructions in geometry accurately, we use a set of tools. Familiarise yourself with these tools:
Ruler (or Straightedge): A ruler has markings (usually in centimetres and inches) along its edge and is used for two main purposes:
- To draw straight lines or line segments.
- To measure the length of a line segment or to mark points at specific distances.

Compass: A compass is a tool used primarily for drawing circles and arcs (parts of a circle). It has two arms joined at a hinge. One arm has a sharp metal needle (or point) at its end, which acts as the center of the circle or arc. The other arm has a holder for a pencil, which draws the curve as the arm is rotated.

Divider: A divider looks similar to a compass but has a sharp point on both arms instead of a pencil holder. It is used for measuring or transferring lengths by setting the distance between its two points. It can also be used to compare the lengths of two line segments directly.
Protractor: A protractor is a semicircular or circular tool marked with degrees, used for measuring existing angles and drawing angles of specific measures.
Set Squares: A set of set squares usually consists of two triangular pieces, one with angles $45^\circ, 45^\circ, 90^\circ$ and the other with angles $30^\circ, 60^\circ, 90^\circ$. They are primarily used for drawing perpendicular lines and parallel lines accurately.
Construction of a Circle
A circle is a set of all points in a plane that are at a fixed distance from a fixed point. The fixed point is called the center, and the fixed distance is called the radius. To construct a circle, you need to know the position of its center and the length of its radius. We use a compass to draw a circle.
Steps to construct a circle of a given radius (e.g., 4 cm):
- Mark a clear point 'O' on your paper using a sharp pencil. This point will be the center of your circle.
- Open the compass to the desired radius (4 cm). Place the metal needle of the compass at the zero mark ($0 \text{ cm}$) of a ruler. Stretch the pencil arm of the compass until the tip of the pencil is exactly at the $4 \text{ cm}$ mark on the ruler. Make sure the compass is held firmly so the opening doesn't change.
- Now, carefully place the metal needle of the compass firmly on the center point 'O' marked on your paper. Press down lightly on the needle point to keep it fixed in place.
- Hold the compass by its upper joint (the hinge) or the handle, and slowly rotate the pencil arm completely around the fixed center 'O'. Keep the pressure on the needle steady so that the center point does not shift, and ensure the compass opening (radius) remains constant.
- The continuous curved line drawn by the pencil will be the required circle with center O and radius 4 cm.


Construction of a Line Segment
A line segment is a part of a line that has two distinct endpoints and a definite length. To construct a line segment of a specific length, we typically use a ruler.
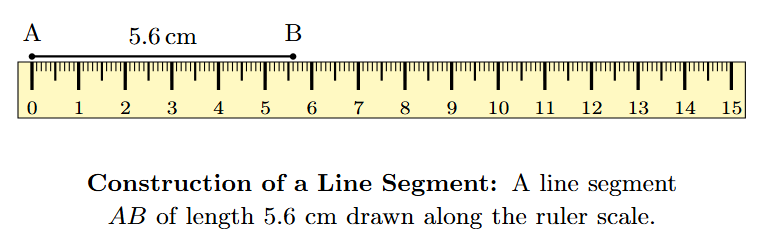
Steps to construct a line segment of a given length (e.g., 5.6 cm):
- Draw a straight line using the edge of a ruler.
- Choose a point on this line and mark it clearly. Label this point 'A'. This will be one endpoint of your line segment.
- Place the ruler along the line you drew, ensuring that the zero mark ($0 \text{ cm}$) on the ruler coincides exactly with point 'A'.
- Look along the ruler to find the marking that corresponds to the desired length (5.6 cm). Mark a point on the line at this marking. Label this point 'B'. This will be the other endpoint of your line segment.
- The part of the line between points A and B is the required line segment of length 5.6 cm.
Constructing a Copy of a Line Segment (Using Compass)
Sometimes, you might need to create a line segment that is an exact copy of an existing line segment without directly measuring its length with a ruler and then drawing a new one. This can be done accurately using only a compass and a straightedge (or ruler for drawing the initial line).
Steps to construct a copy of a given line segment $\overline{AB}$
You are given a line segment $\overline{AB}$.
Draw a line $l$ using a ruler. This line should be longer than the segment you expect to copy.
Mark a point 'C' on the line $l$. This will be the starting point of your copied segment.
Take your compass. Carefully place the metal needle at point 'A' of the given line segment $\overline{AB}$. Adjust the compass opening so that the pencil tip is exactly on point 'B'. The distance between the needle and the pencil tip is now equal to the length of $\overline{AB}$.

Without changing the compass opening (which represents the length of $\overline{AB}$), lift the compass and place the metal needle at point 'C' on line $l$.
Draw an arc that intersects the line $l$ at a point. Label this intersection point 'D'.
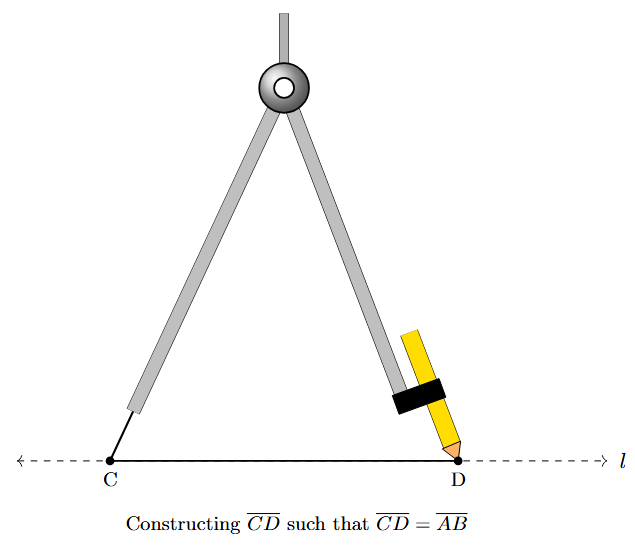
The line segment $\overline{CD}$ is an exact copy of the line segment $\overline{AB}$. Their lengths are equal: length of $\overline{CD}$ = length of $\overline{AB}$.
Construction of Perpendicular
In geometry, lines and segments can have various relationships. One important relationship is perpendicularity. Two lines are Perpendicular if they intersect at a right angle ($90^\circ$). Being able to accurately construct perpendicular lines and perpendicular bisectors using geometric tools is a fundamental skill in practical geometry.
Constructing a Perpendicular to a Line Through a Point on the Line
Sometimes we need to draw a line that forms a $90^\circ$ angle with a given line and passes through a specific point that lies on that line. We can achieve this precisely using a ruler and compass.
Steps to construct a perpendicular to a line $l$ through a point P on $l$:
- Draw a straight line $l$ and clearly mark a point 'P' somewhere on this line.
- With 'P' as the center, take the compass and draw an arc with a convenient radius. The radius should be chosen so that the arc intersects the line $l$ on both sides of point P. Label the two points where the arc intersects line $l$ as 'A' and 'B'.
- Now, with 'A' as the center and a radius greater than the length of AP (or PB, since AP=PB), draw an arc. Draw this arc on one side of the line $l$, typically above the line.
- Next, with 'B' as the center and using the exact same radius as used in step 3, draw another arc on the same side of the line $l$ (above the line). These two arcs (from A and B) should intersect at a point. Label this intersection point 'Q'.
- Finally, draw a straight line passing through points P and Q using a ruler.
- The line PQ is perpendicular to line $l$ at point P. You can verify this by placing a protractor with its center at P and checking that the angle formed by PQ and $l$ is $90^\circ$.





Constructing a Perpendicular to a Line Through a Point Not on the Line
We might also need to construct a line perpendicular to a given line that passes through a point that is not located on the line itself. This is like dropping a perpendicular from a point to a line.
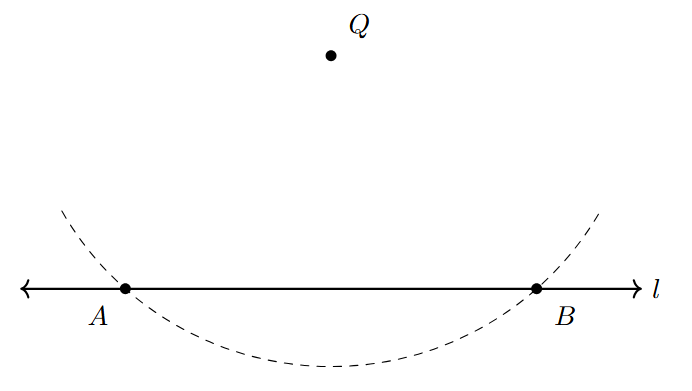
Steps to construct a perpendicular to line $l$ through a point Q not on $l$:
- Draw a straight line $l$ and mark a point 'Q' that is not on the line $l$. Point Q can be above or below the line.
- With 'Q' as the center, take your compass and draw an arc with a radius large enough to intersect the line $l$ at two distinct points. Label these intersection points as 'A' and 'B'.
- Now, with 'A' as the center, take a radius that is greater than half the length of the segment AB. Draw an arc on the side of the line $l$ opposite to point Q. (If Q is above $l$, draw arcs below $l$; if Q is below $l$, draw arcs above $l$).
- Next, with 'B' as the center and using the exact same radius as used in step 3, draw another arc on the same side of line $l$. These two arcs (from A and B) should intersect at a point. Label this intersection point 'R'.
- Draw a straight line passing through points Q and R using a ruler.
- The line QR is perpendicular to line $l$. The point where QR intersects $l$ is the foot of the perpendicular from Q to $l$.



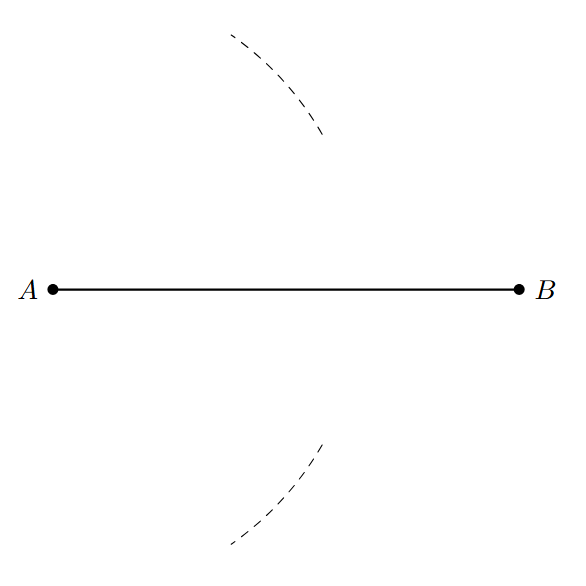
Constructing a Perpendicular Bisector of a Line Segment
A Perpendicular Bisector of a line segment is a line that satisfies two conditions:
- It is perpendicular ($90^\circ$) to the line segment.
- It passes through the midpoint of the line segment, dividing it into two equal halves.
Constructing a perpendicular bisector is useful for finding the midpoint of a segment or for constructions related to circles and triangles.
Steps to construct the perpendicular bisector of a line segment AB:
- Draw a line segment AB of any length.
- With 'A' as the center, take the compass and set the radius to be more than half the length of the line segment AB. This is important for the arcs to intersect later. With this radius, draw an arc above the line segment AB and another arc below the line segment AB.
- Now, with 'B' as the center and using the exact same radius as used in step 2, draw another arc above the line segment AB and another arc below the line segment AB. These two arcs (from B) should intersect the previously drawn arcs (from A) at two distinct points. Label the intersection point above AB as 'P' and the intersection point below AB as 'Q'.
- Draw a straight line passing through points P and Q using a ruler.
- The line PQ is the perpendicular bisector of the line segment AB. It is perpendicular to AB, and the point where PQ intersects AB is the midpoint of AB.



Construction of Angles
In geometry, we frequently work with angles. Angles are formed by two rays starting from a common point (the vertex). In practical geometry, we learn how to draw angles of specific measures accurately. We can do this using a protractor for any angle measure, or for certain specific angles, we can use just a compass and ruler, which gives very precise constructions.
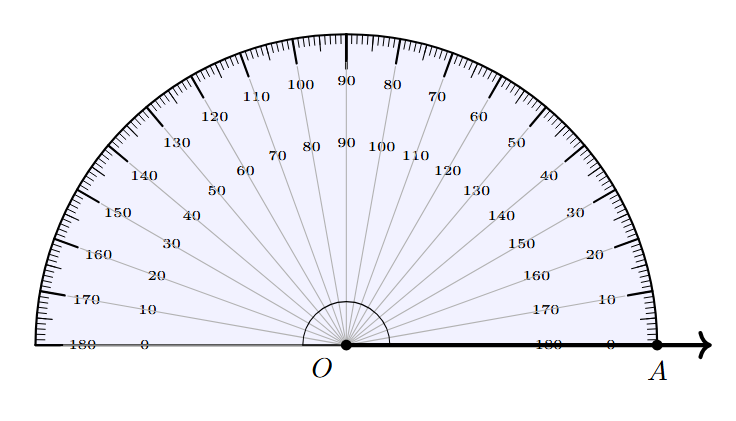
Constructing an Angle Using a Protractor
A protractor is a tool designed specifically for measuring and drawing angles. It is usually semicircular (180 degrees) and has markings along its curved edge indicating degrees.
Steps to construct an angle of a given measure (e.g., $75^\circ$) using a protractor:
- Draw a straight line segment or a ray on your paper using a ruler. Label the starting point (vertex) as 'O' and another point on the ray as 'A'. This forms one arm of the angle, ray OA.
- Place the protractor on the ray OA such that the center point of the protractor (usually marked by a small hole or crosshairs at the middle of the straight edge) coincides exactly with the vertex 'O'. Align the base line (the straight edge) of the protractor precisely along the ray OA. Make sure the 0-degree mark on the protractor is on the ray OA.
- Now, locate the desired angle measure on the curved edge of the protractor. Since ray OA is aligned with the 0-degree mark on the right side of the protractor, use the inner scale (the scale that starts from 0 on the right). Find the marking for $75^\circ$ on this scale. Place a sharp pencil point on your paper at this $75^\circ$ mark and make a small dot. Label this point 'B'.
- Remove the protractor from the paper.
- Using a ruler, draw a straight line segment or a ray from the vertex 'O' to the marked point 'B'. This forms the second arm of your angle, ray OB.
- The angle formed, $\angle \text{AOB}$, is the required angle with a measure of $75^\circ$.
- If the ray OA is aligned with the 0-degree mark on the left side of the protractor, you would use the outer scale.


Constructing Specific Angles Using Compass and Ruler (Without Protractor)
Certain angles can be constructed very accurately using only a compass and a ruler (as a straightedge). These constructions are based on the properties of equilateral triangles and perpendicular lines.
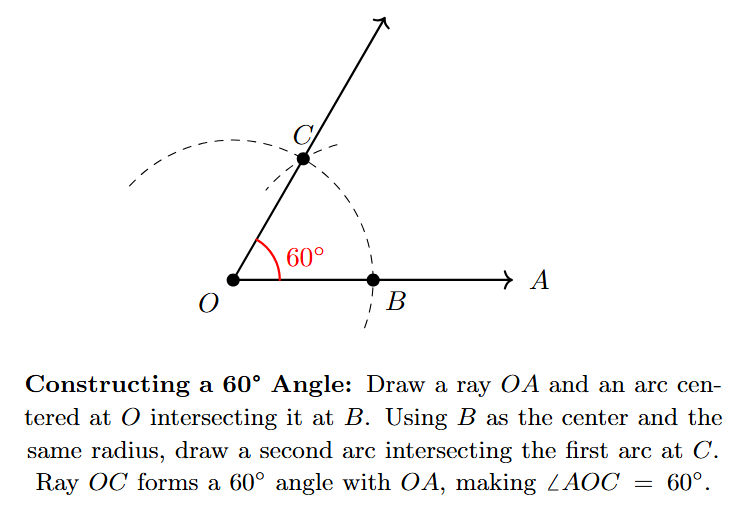
Constructing a $60^\circ$ Angle
A $60^\circ$ angle is fundamental because the angles in an equilateral triangle are all $60^\circ$. This construction basically creates part of an equilateral triangle.
Steps to construct a $60^\circ$ angle at point O on ray OA:
- Draw a ray OA. Point O is where the angle will be formed.
- With 'O' as the center, draw an arc using the compass with a convenient radius. This arc should intersect ray OA at a point. Label this intersection point 'B'.
- Now, with 'B' as the center, and keeping the exact same radius that you used in step 2, draw another arc. This second arc should intersect the first arc (the one centered at O) at a point. Label this intersection point 'C'.
- Draw a ray from the vertex 'O' passing through the point 'C'. Label this ray OC.
- The angle $\angle \text{AOC}$ formed by rays OA and OC is a $60^\circ$ angle. The triangle OBC formed has sides OB, BC, and OC all equal to the radius used, making it an equilateral triangle. Thus, $\angle \text{AOC} = 60^\circ$.


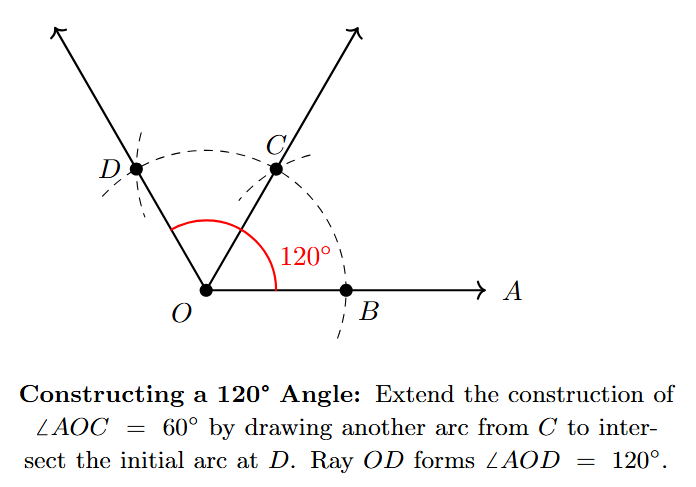
Constructing a $120^\circ$ Angle
A $120^\circ$ angle is twice the measure of a $60^\circ$ angle. We can construct it by extending the $60^\circ$ construction.
Steps to construct a $120^\circ$ angle at point O on ray OA:
- Follow steps 1 and 2 of the $60^\circ$ construction. Draw a ray OA. With O as the center and a convenient radius, draw a large arc that intersects ray OA at a point, let's call it B.
- With 'B' as the center and the same radius, draw an arc intersecting the first arc (from O) at a point 'C'. If we draw ray OC, then $\angle \text{AOC} = 60^\circ$.
- Now, with 'C' as the center and using the exact same radius, draw another arc intersecting the first main arc (the one drawn from O) at a new point. Label this point 'D'. This second cut on the arc marks the $120^\circ$ point.
- Draw a ray from the vertex 'O' passing through the point 'D'. Label this ray OD.
- The angle $\angle \text{AOD}$ formed by rays OA and OD is a $120^\circ$ angle. This is because $\angle \text{AOC} = 60^\circ$ and $\angle \text{COD} = 60^\circ$ (based on the construction using equilateral triangle principles), and thus $\angle \text{AOD} = \angle \text{AOC} + \angle \text{COD} = 60^\circ + 60^\circ = 120^\circ$.

Constructing a $90^\circ$ Angle
A $90^\circ$ angle, or a right angle, can be constructed by bisecting the angle between the $60^\circ$ and $120^\circ$ marks. This method builds directly upon the construction of the $120^\circ$ angle.
Steps to construct a $90^\circ$ angle at point O on ray OA:
- First, follow the steps to mark the $60^\circ$ and $120^\circ$ angles. You will have a ray OA, a vertex O, a main arc, a point 'C' on the arc representing the $60^\circ$ mark, and a point 'D' on the same arc representing the $120^\circ$ mark. Do not draw the rays OC and OD yet.
- The angle between the $60^\circ$ mark (point C) and the $120^\circ$ mark (point D) is $120^\circ - 60^\circ = 60^\circ$. We will bisect this angle, $\angle \text{COD}$, to get a $30^\circ$ angle.
- With 'C' as the center and any radius greater than half the distance between C and D, draw an arc in the interior of $\angle \text{COD}$.
- With 'D' as the center and using the exact same radius as in the previous step, draw another arc that intersects the first arc. Label the point of intersection 'E'.
- Draw a ray from the vertex 'O' passing through the point 'E'. Label this ray OE.
- The angle $\angle \text{AOE}$ is the required $90^\circ$ angle.
Justification: Ray OE bisects $\angle \text{COD}$. Therefore, $\angle \text{COE} = \frac{1}{2}\angle \text{COD} = \frac{1}{2}(60^\circ) = 30^\circ$. The final angle is the sum of the initial $60^\circ$ and this new $30^\circ$: $\angle \text{AOE} = \angle \text{AOC} + \angle \text{COE} = 60^\circ + 30^\circ = 90^\circ$.
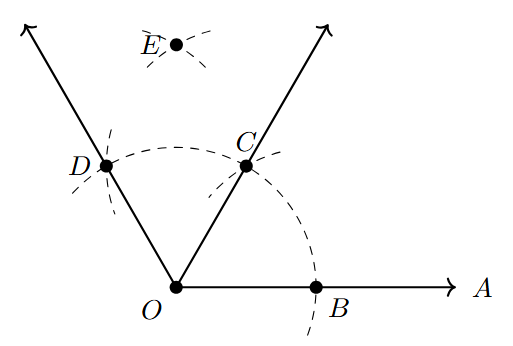

Bisecting an Angle
To Bisect an Angle means to divide the angle into two angles of equal measure. An angle bisector is a ray that originates from the vertex of the angle and divides it into two equal parts. We can bisect any angle using a compass and ruler.
Steps to bisect angle $\angle \text{ABC}$ (or any angle with vertex B):
- Draw the angle $\angle \text{ABC}$ using a protractor or freehand. Vertex is B, arms are rays BA and BC.
- With 'B' as the center, draw an arc using the compass with a convenient radius. This arc should intersect both arms of the angle, ray BA and ray BC. Label the point where the arc intersects ray BA as 'P', and the point where it intersects ray BC as 'Q'.
- Now, with 'P' as the center and a radius greater than half the length of the segment PQ, draw an arc. Draw this arc in the interior (inside) of the angle $\angle \text{ABC}$.
- Next, with 'Q' as the center and using the exact same radius as used in step 3, draw another arc. This arc should also be drawn in the interior of the angle and should intersect the arc drawn from P. Label the intersection point of these two arcs as 'R'.
- Draw a ray from the vertex 'B' passing through the point 'R'. Label this ray BR.
- The ray BR is the angle bisector of $\angle \text{ABC}$. It divides the angle $\angle \text{ABC}$ into two equal angles: $\angle \text{ABR}$ and $\angle \text{RBC}$. You can check with a protractor that $\angle \text{ABR} = \angle \text{RBC} = \frac{1}{2} \angle \text{ABC}$.




Constructing Other Angles by Bisecting or Combining
Once you know how to construct basic angles like $60^\circ$ and $90^\circ$ and how to bisect any angle, you can construct many other angles accurately using just a compass and ruler. This is done by finding half of existing angles (bisecting) or by adding angles together.
-
Constructing a $30^\circ$ angle:
A $30^\circ$ angle is half of a $60^\circ$ angle ($30^\circ = \frac{60^\circ}{2}$).
- First, construct a $60^\circ$ angle.
- Then, bisect the $60^\circ$ angle.
- The resulting angle between the base ray and the bisector is $30^\circ$.
-
Constructing a $45^\circ$ angle:
A $45^\circ$ angle is half of a $90^\circ$ angle ($45^\circ = \frac{90^\circ}{2}$).
- First, construct a $90^\circ$ angle.
- Then, bisect the $90^\circ$ angle.
- The resulting angle between the base ray and the bisector is $45^\circ$.
-
Constructing a $15^\circ$ angle:
A $15^\circ$ angle is half of a $30^\circ$ angle ($15^\circ = \frac{30^\circ}{2}$).
- First, construct a $60^\circ$ angle and bisect it to get a $30^\circ$ angle.
- Then, bisect the $30^\circ$ angle.
- The resulting angle is $15^\circ$.
-
Constructing a $75^\circ$ angle:
A $75^\circ$ angle is located halfway between $60^\circ$ and $90^\circ$ ($75^\circ = 60^\circ + 15^\circ$).
- Construct a $90^\circ$ angle. This process also gives you the arc mark for the $60^\circ$ angle.
- Identify the two points on the main arc that represent $60^\circ$ and $90^\circ$.
- Bisect the $30^\circ$ angle between these two marks.
- Draw a ray from the vertex through this new bisection point. The angle formed with the base ray is $75^\circ$.
-
Constructing a $105^\circ$ angle:
A $105^\circ$ angle is located halfway between $90^\circ$ and $120^\circ$ ($105^\circ = 90^\circ + 15^\circ$).
- Construct a $120^\circ$ angle, which gives you marks for $60^\circ$ and $120^\circ$. Then, construct a $90^\circ$ angle on the same vertex.
- Identify the two points on the main arc that represent $90^\circ$ and $120^\circ$.
- Bisect the $30^\circ$ angle between these two marks.
- Draw a ray from the vertex through this new bisection point. The angle formed with the base ray is $105^\circ$.
-
Constructing a $150^\circ$ angle:
A $150^\circ$ angle is located halfway between $120^\circ$ and $180^\circ$ ($150^\circ = 120^\circ + 30^\circ$).
- Draw a straight line, which represents a $180^\circ$ angle. Mark the vertex O on it.
- From the vertex O, construct a $120^\circ$ angle.
- Identify the points on the arc representing $120^\circ$ and $180^\circ$ (where the arc meets the straight line).
- Bisect the $60^\circ$ angle between these two marks.
- Draw a ray from the vertex through this new bisection point. The angle formed with the base ray is $150^\circ$.
By repeatedly bisecting and combining these fundamental angles, you can construct many other angles like $22.5^\circ$ (by bisecting $45^\circ$). However, constructing arbitrary angles (like $10^\circ$ or $23^\circ$) without a protractor is generally not possible with just a compass and ruler.

